[비율검정] 두 그룹의 비율 차를 이용한 검정

 

오늘은 두 그룹의 비율 차이 검정에 대해 정리하고자 한다.

분석코드 및 대부분의 내용은 'Machine Learning at Work 머신러닝 실무 프로젝트' 책을 참고하였습니다.

 

두 개의 광고 서비스를 통해 각각 유입된 사용자들의 이용률을 아래와 같이 얻었다고 하자.

광고종류	유입 사용자 수	지속 이용 사용자 수	지속 이용 전환율
A	205	40	19.5%
B	290	62	21.4%

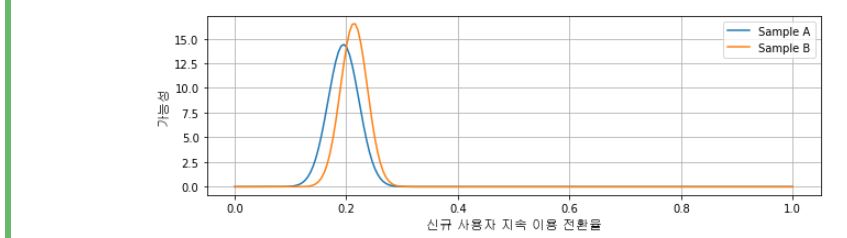
위의 예시는 '지속이용자' 와 '이탈자' 두 범주에 대한 비율을 보이고 있기 때문에 이항분포를 따르지만 유입 사용자수가 어느정도로 크기 때문에 정규분포를 따른다고 보고 지속 이용 전환율의 분포를 시각화해보자.

(위 내용은 중심극한 정리 참고!!)

import matplotlib.pyplot as plt
import matplotlib
from scipy.stats import norm
import matplotlib.font_manager as fm
 
# 테스트 데이터. [지속 이용 전환 , 이탈 수]
a = [40, 165]
b = [62, 228]
 
print('Sample A: size={}, converted={}, mean={:.3f}'.format(sum(a), a[0], a[0]/sum(a)))
print('Sample B: size={}, converted={}, mean={:.3f}'.format(sum(b), b[0], b[0]/sum(b)))
 
x = np.linspace(0, 1, 200)
 
# 표본 A로부터 유입
n = sum(a)
p = a[0]/n
std = np.sqrt(p*(1-p)/n)
y_a = scipy.stats.norm.pdf(x, p, std)
 
# 표본 B로부터 유입
n = sum(b)
p = b[0]/n
std = np.sqrt(p*(1-p)/n)
y_b = scipy.stats.norm.pdf(x, p, std)
 
font_path = 'C:/Windows/Fonts/gulim.ttc'
fontprop = fm.FontProperties(fname=font_path, size=12)
 
plt.figure(figsize=(10, 3))
plt.plot(x, y_a, label='Sample A')
plt.plot(x, y_b, label='Sample B')
plt.legend(loc='best')
plt.xlabel('신규 사용자 지속 이용 전환율', fontproperties=fontprop)
plt.ylabel('가능성',fontproperties=fontprop)

np.linspace 함수는 선형구간을 지정한 수만큼 반환해주는 함수로 0과 1사이에서 200개 구간으로 나누었다.

그래프의 Y라벨과 X라벨에 한글 폰트로 지정하기 위해서는 먼저 한글폰트가 설치 되어 있어야 한다.

(저작권 걱정없는 무료 한글폰트 ← 들어가시면 여러 무료 폰트 받을 수 있습니다!!)

font_path와 fontprop를 지정하고, plt.xlabel과 plt.ylabel에 fontproperties = fontprop 추가한다.

 

그림을 보면, Sample B의 지속 이용 전환율이 조금 더 높아 보이지만 결론을 내리기에는 애매한 부분이 있으므로 Sample A와 Sample B의 전환율 차이가 있는지 카이제곱 검정을 통해 알아보자.

광고종류	지속 이용 사용자 수	이탈 수
A	40	165
B	62	228

# 카이제곱 검정
_, p_value, _, _ = scipy.stats.chi2_contingency([a, b])
print(p_value)
 

scipy.stats.chi2_contingency는 카이제곱 통계량, p-value, 자유도 등을 Return 해주고,

print(scipy.stats.chi2_contingency.__doc__  를 통해 자세한 내용을 확인할 수 있다.

 

p-value : 0.694254736449269

유의수준 0.05보다 크므로 귀무가설(Sample A와 Sample B 모집단은 지속 이용 전환율이 같다)을 기각할 수 없다. 즉, 모집단 Sample A와 모집단 Sample B의 지속 이용 전환율은 다르지 않다라고 결론 지을 수 있다.

 

 

※ 카이제곱 검정

두 변수 사이에 연관성이 있는가 관심이 있는 경우 변수가 명목척도를 이용하여 측정되었을 때 통상적으로 카이제곱 검정을 사용한다.

수집한 표본이 모집단의 분포와 같은지 다른지 검정할 때 쓰이며 주로 독립성 검정, 동일성 검정, 적합성 검정에 사용된다.

 

 

 

감사합니다 :)