아래 내용은 XAI를 공부하며 'XAI 설명 가능한 인공지능, 인공지능을 해부하다' 서적을 요약 정리한 내용입니다. 실습을 통해 본 컴퓨터 세팅에 따라 코드 부분이 다를 수 있습니다.

연관게시글
실습1 : 피마 인디언 당뇨병 결정 모델
이번 장은 실습 데이터를 가지고 간단한 실험을 해보겠습니다. 데이터 이름은 '피마 인디언 당뇨병 진단'으로 세계에서 당뇨병 발병 비율이 가장 높은 애리조나 주의 피마 인디언을 대상으로 조사한 자료입니다. 자료 속정은 8가지로 다음과 같습니다.
1. 임신 횟수
2. 경구 포도당 내성 검사에서 혈장 포도당 농도(2시간 이후 측정)
3. 확장기 혈압(mmHg)
4. 삼두근 피부 두께(mm)
5. 인슐린 혈청(μU/ml) 저항성(2시간 이후 측정)
6. 체질량 지수 BMI
7. 당뇨병 병력 함수
8. 나이(세)
이 여뎗 가지 피처를 바탕으로 당뇨병 진단 결과가 이진수로 주어지며 0은 당뇨병이 아님, 1은 당뇨병을 의미합니다.
1. 학습하기
데이터는 캐글에서 직접 내려받을 수 있습니다. Xgboost 알고리즘을 사용하여 모델을 만들어 보겠습니다.
import pandas as pd
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from xgboost import XGBClassifier
# 데이터 로드
dataset = pd.read_csv('./diabetes.csv')
# X와Y로 분리
X = dataset.iloc[:,0:8]
y = dataset.iloc[:, 8]
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=7)
# 학습 데이터로 모델을 학습시키기
model = XGBClassifier()
model.fit(x_train, y_train)
# 예측하기
y_pred = model.predict(x_test)
predictions = [round(value) for value in y_pred]
# 평가하기
accuracy = accuracy_score(y_test, predictions)
print('Accuracy : %.2f%%'%(accuracy*100))# 결과
Accuracy : 81.17%학습한 모델은 81.17%의 정확도를 갖고 있는 것으로 나옵니다. 그러면 다음 코드를 입력해서 데이터 하나에 대한 정확도를 확인해보겠습니다.
value = pd.DataFrame([[1, 161, 72, 35, 0, 28.1, 0.527, 20]], columns = x_train.columns.tolist())
l = model.predict_proba(value)
print('No diabetes : {:.2%}\nYes diabetes : {:.2%}'.format(l[0][0], l[0][1]))No diabetes : 69.09%
Yes diabetes : 30.91%위 코드를 실행하면 학습된 모델이 특정 환자에 대해 당뇨병이 아니라고 진단할 확률이 69.09%이고, 당뇨병이라고 진단할 확률은 30.91%입니다. 모델이 특정 환자에 대해서 어떻게 당뇨병이 없을 것이라고 진단하였는지는 2절 의사 결정 트리에서 확인해보도록 하겠습니다.
일반적인 학습 모델은 위의 과정을 통해 완성되고 그대로 사용됩니다. 그러나 81.17%의 모델 정확도가 부족하다고 느끼는 분들은 파라미터 튜닝으로 테스트 정확도를 올리려고 할 것입니다. 그렇지만 파라미터 튜닝만으로는 위 모델이 어떤 원리로 환자를 당뇨라고 진단하는지 8개의 피처의 우선순위는 어떻게 구성되는지 그리고 각 피처의 수치 변화에 따라 당뇨병 진단 가능성은 어떻게 변화하는지 등에 대한 질문에는 답할 수 없을 것입니다. 이런 상황에서 XAI 기법을 결합하면 더운 현실적인 질문에 대답할 근간을 마련할 수 있습니다.
2. 설명 가능한 모델 결합하기
L1, L2 등의 파라미터 튜닝은 모델의 테스트 정확도는 올릴 수 있을지언정 모델의 당뇨병 진단 이유를 설명할 수 없습니다.
2.1. 의사 결정 트리 시각화
파이썬 패키지인 Graphviz를 사용하여 XGBoost로 생성한 모델에 대해 의사 결정 트리를 시각해보겠습니다. 아래 코드를 실행하니 graphviz 패키지를 설치하라는 오류가 나서 설치를 우선 진행하고 다시 실행하였습니다.
conda install graphviz python-graphviz%matplotlib inline
from xgboost import plot_tree
import matplotlib.pyplot as plt
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 100, 200
# 의사 결정 트리 시각화
plot_tree(model)
plt.show()%matplotlib inline 명령어는 ipython notebook에서 결과로 나타나는 미디어(음악, 그림, 애니메이션)를 현재 브라우저에서 표현하는 명령어입니다.
저는 Graphviz 패키지를 설치하고 실행했을때 에러가 나지 않았지만 만약 런타임 에러가 발생한다면 추가로 프로그램 설치와 파이썬 경로 설정이 필요합니다. 설치는 위의 코드로 설치하면 되며 경로 설정은 아래 코드와 같이 환경 변수를 추가해주시면 됩니다. (참고 : stackoverflow)
import os
# 경로설정하기
os.environ['PATH']+=(os.pathsep + 'C:/Program Files (x86)/Graphviz2.38/bin/')rcParams는 matplotlib에서 보여주는 차트의 시각화 옵션을 다시 설정합니다. figure.figsize는 그림의 가로, 세로를 인치 단위로 조정하는 파라미터로 이밖에 다른 옵션은 공식 문서에서 확인할 수 있습니다. (참고 : matplotlib.org)

[그림1]을 해석해보면 루트 노드는 GTT 테스트 결과가 128 미만인지를 묻고 있으며 수치가 128 미만이거나 데이터가 존재하지 않는다면, 'yes, missing'을 그렇지 않으면 'no'를 따라 오른쪽 노드로 나뉩니다.
'의사 결정 트리'는 초반에 분류되는 노드의 정보 이득량이 가장 많은데 위 당뇨병 진단 모델은 GTT 테스트 수치를 1순위로 진단하고 있는 것을 알 수 있습니다.
위의 특정 환자를 대입해보면 GTT 수치는 161로 128보다 크므로 'no'를 따라 오른쪽으로 이동하겠습니다.
다음 노드에서는 BMI 수치를 묻고 있으며 특정 환자의 BMI 수치는 28.1로 29.95보다 작으므로 'yes, missing'을 선택하게 됩니다. 의사 결정 트리가 다시 GTT 수치 162보다 작은지 묻게 되는데 특정 환자의 수치는 161이므로 'yes, missing'을 선택하여 마지막 노드에서 leaf=-0.112000003의 값을 가지며 종료됩니다. 마지막 leaf 값은 로지스틱 함수 확률값으로 0은 중립, 음수는 당뇨병 없음, 양수는 당뇨병 있음을 진단합니다.
$$ p(x) = \frac{1}{1+e^{-leafvalue}} $$
leaf value에 -0.11200003을 넣고 계산하면 0.472가 나오는데 로지스틱 임계값 0.5를 넘지 않아 당뇨병을 앓고 있지 않다고 진단합니다.
2.2. 피처 중요도 구분하기
피처 중요도란 해당 피처가 모델의 에러를 얼마나 줄여주는지를 근거로 중요성을 측정하는 방법입니다. 모델의 피처 중요도를 계산하고 시각화 해보겠습니다.
from xgboost import plot_importance
rcParams['figure.figsize'] = 10, 10
plot_importance(model)
plt.yticks(fontsize=15)
plt.show()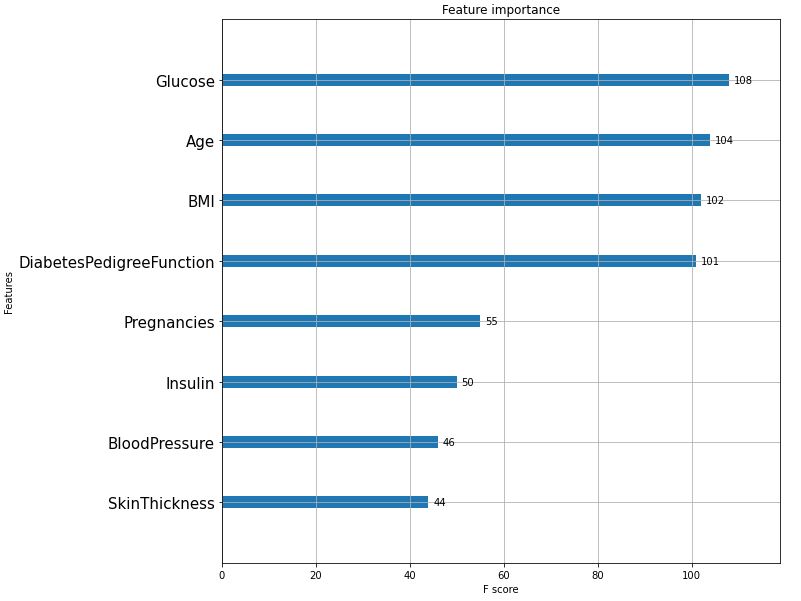
[그림2] 트리에서 최상단 분기점 GTT 수치와 동일하게 피처 중요도 그래프에서도 글루코스(Glucose) 피처가 당뇨병을 진단하는데 가장 중요한 요소라고 드러났습니다. 일반적으로는 대부분 일치하지만 꼭 피처 중요도의 순서가 의사 결정 트리의 순서를 결정하는 것은 아닙니다. 왜냐하면 의사 결정 트리의 노드는 선정과 분기 기준이 정보 이득이 큰 방향이고, 피처 중요도는 모델의 분류 에러가 큰 순서로 정렬되기 때문입니다.
2.3. 부분 의존성 플롯 그리기
부분 의존성 플롯은 피처의 수치 변화에 따라 모델에 기여하는 정도가 어떻게 달라지는지 확인할 수 있는 XAI 기법입니다. 앞서 피처 중요도로 모델이 피처를 어떻게 해석하는지 살펴보았으나 해당 피처가 모델의 판단에 긍정적인 영향을 미치는지, 부정적인 영향을 미치는지 알 수 없습니다. 또한 현실 세계에서 다수의 피처들은 서로 독립이 아닙니다.
부분 의존성 플롯은 피처가 모델에 긍정/부정적인 영향을 미치는지 파악하게 도울뿐만 아니라, 특정 피처에 대해 여유분을 함께 표시함으로써 피처 간 독립을 보장하지 못하는 환경에서 어느 정도 모델에 오차가 있을 수 있는지를 확인할 수 있게 해줍니다.
부분 의존성 플롯은 파이썬 패키지 pdpbox로 간단하게 사용할 수 있습니다. 자세한 내용은 공식 문서를 참고바라며, pdpbox의 장점은 다음과 같습니다.
1. 기본 부분 의존성 플롯뿐만 아니라 목표 플롯, 모델 예측에 대한 의존성 플롯, 두 피처 간 의존성 플롯 비교 등 가능
2. 단일 예측뿐만 아니라 멀티 클래스 분류기에도 작동
3. 두 개의 피처가 상호 작용하는 부분 의존성 플롯도 함께 시각화 가능
1) 목표 플롯 그리기(Target plots)
피마 인디언 당뇨 분류 모델에 pdpbox를 작용해보겠습니다.
! conda install -c conda-forge pdpbox
from pdpbox import info_plots
pima_data = dataset.copy()
pima_features = dataset.columns[:8]
pima_target = dataset.columns[8]
fig, axes, summary_df = info_plots.target_plot(
df = pima_data,
feature = 'Glucose',
feature_name = 'Glucose',
target = pima_target)info_plots.target_plot 메서드를 보면 학습한 모델을 파라미터로 받고 있지 않습니다. 부분 의존성 기법은 학습 데이터를 철저하게 분석해서 모델이 어떻게 학습할 것인지 예상하는 기법입니다. 예를들어 카테고리가 3가지인 데이터를 모델링할 경우 3개의 레이블링 된 데이터의 비율은 비슷해야 합니다. 그렇지 않고 불균형하다면 모델은 과적합될 것입니다. 피처 또한 마찬가지입니다. 특정 데이터가 편향돼 있고, 그 데이터에 맞춰 결론이 왜곡돼 있다면 모델을 뜯어보지 않아도 어떤 편향으로 모델이 학습될지 파악할 수 있습니다.
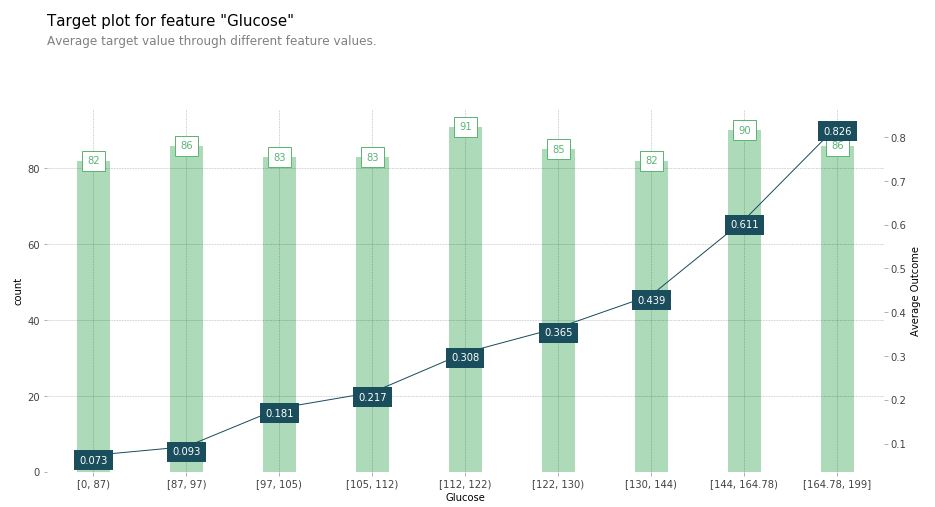
[그림3]을 해석해봅시다. X축은 GTT 수치, 왼쪽 Y축은 각 수치 구간별 데이터 개수, 오른쪽 Y축은 당뇨병 진단 여부(>50%)입니다. 막대그래프는 왼쪽 Y축에 대응하고, 꺽은선 그래프는 오른쪽 Y축에 대응합니다. 예를들어 GTT가 84mg/dL인 경우 데이터가 속한 그룹은 맨 왼쪽 첫 번째 막대그래프에 속하며 데이터 수는 82개 입니다. 또한 GTT가 84mg/dL인 환자에 대해 수치만 관찰했을 때 당뇨를 진단할 확률은 오른쪽 Y축에 대응하며, 확률은 평균 7.3%입니다.
이제 이 그래프를 의사에게 가져갔다고 했을 때 의사는 이 모델이 충분히 합리적이라고 판단할 것입니다. 당뇨병 진단 기준은 공복혈당이 126mg/dL이거나 GTT 2시간 이후 혈당이 200mg/dL이기 때문입니다. 따라서 의사는 GTT 수치가 커질수록 당뇨병 진단 가능성이 점점 올라가는 모델이 자연스럽다고 받아드리게될 것입니다.

이번에는 BloodPressure로 바꿔서 보겠습니다. 고혈압의 진단 범위는 80-120mmHg 이상일 때이나 최대값인 122mgHg인 환자에 대해서 당뇨병 진단 가능성이 50%가 넘지 않습니다. 따라서 혈압 피처만으로 당뇨병을 진단하는 것은 섣부르다고 결론 지을 수 있습니다.
2) 예측 분포 플롯 그리기(Prediction distribution plots)
데이터와 실제 모델을 결합해 두 결과가 일치하는지 확인해봅시다. 이 기법은 예측 분포 플롯이라고 부릅니다.
fig, axes, summary_df = info_plots.actual_plot(
model = model,
X = pima_data[pima_features],
feature = 'Glucose',
feature_name = 'Glucose',
predict_kwds = {}
)
앞서 info_plots.target_plot과 다른 점은 메서드의 파라미터로 우리가 학습한 모델이 들어간다는 점입니다. 이 메서드는 모델이 학습 데이터의 빈도와 비슷한 추이로 당뇨병을 진단하는가를 예측합니다. 위의 분포에는 캔들스틱 차트가 포함되는데 '모델'이 특정 수치를 보이는 환자들에 대해 당뇨병이 있으리라 추정하는 차트입니다.
GTT 수치가 0-87mg/dL 구간에 있는 환자들의 결과를 비교해보면 1번 목표 플롯에서는 약 7.3%의 가능성으로 당뇨 진단을 추정하지만 모델의 경우 평균 5.2% 확률로 당뇨병을 앓고 있다고 추정하고 있습니다. 머신러닝 결과 GTT 수치 0-87mg/dL 구간 환자는 데이터를 단순하게 사용했을 때 보다 당뇨병의 존재 가능성이 상대적으로 더 낮아졌음을 알 수 있고 해당 구간의 GTT 피처는 당뇨병을 진단하는데 있어 음의 상관관계를 가진다고 할 수 있습니다.
3) 모델 부분 의존성 플롯
from pdpbox.pdp import pdp_isolate, pdp_plot
pdp_gc = pdp_isolate(
model = model,
dataset = pima_data,
model_features = pima_features,
feature = 'Glucose')
# 플롯 정보 설정
fig, axes = pdp_plot(
pdp_gc,
'Glucose',
plot_lines = False,
frac_to_plot = 0.5,
plot_pts_dist = True)pdp_isolate 메서드는 Glucose 피처 하나에 대해 부분 의존성 수치를 계산하여 반환하고 pdp_plot 메서드를 호출하여 플롯을 그릴 수 있습니다. plp_plot은 파라미터로 PDPIsolate 객체와 피처 이름 plot_lines, frac_to_plot, plot_pts_dist 등을 받습니다.


plot_lines는 차트의 옅은 푸른색 영역으로 이 항목을 True로 바꾸면 [그림6] 오른쪽 차트와 같이 매회에 대응하는 별도의 라인으로 표시됩니다. [그림6] 왼쪽 차트는 간결한 반면 150-175mg/dL 사이의 추세가 급격히 올라가는 부분을 발견할 수는 없습니다. 해당 내용을 [그림6] 왼쪽 차트에서 확인할 수 없는 이유는 특정 부분 의존성 계산 결과가 해당 구간에 미치는 영향이 미미했기 때문입니다. plot_pts_dist는 특정 피처에 대해 데이터가 얼마나 분포하는지를 세로 막대로 표시합니다.
4) 혈압과 GTT 테스트 결과 간 부분 의존성 플롯
pdp_interact는 메서드 파라미터로 모델과 데이터, 특정 부분 의존성 피처를 받아서 pdp_interaction에 저장합니다.


[그림7]의 X축은 혈압, Y축은 GTT 테스트 결과로 색이 옅어질수록 당뇨병 진단 모델의 가능성이 올라갑니다. 왼쪽 차트에서 등고선은 대체로 X축에 평행하는데 이는 당뇨병 진단 모델이 혈압보다는 GTT 테스트에 더 의존적임을 의미합니다. 다만 혈압이 80-122mmHg이면서 GTT 테스트 결과가 100-130mg/dL인 구간 사이에서는 종 모양 그래프가 관찰되는데 해당 구간 안에서는 혈압의 변화가 당뇨병 예측 결과에 민감하게 영향을 받고 있음을 의미합니다.
오른쪽 차트는 plot_type='grid'로 바꾼 격자 차트로 두 피처의 변화량이 모델의 예측 결과에 얼마나 큰 영향을 미치는 판단합니다. 해당 그림으로 확인한 결과 부분 의존성 차트는 모델이 혈압보다는 GTT 테스트 피처의 크기 변화에 훨씬 더 민감하게 당뇨병 진단을 내리는 것처럼 해석됩니다.
2.4. 마무리
피처 중요도는 각 피처가 모델에 미치는 영향력을 절댓값으로 계산한 것이고, 목표 플롯은 피처의 구간별 분포에 대한 결과 간 상관관계 분석 결과를, 부분 의존성 플롯은 학습한 모델에 대해 구간별로 해석 결과를 시각화합니다.
XAI는 모델을 해석하는 다양하고 합리적인 관점을 제시합니다. XAI는 학습된 모델이 어떤 영역에서 강점과 약점이 있는지 파악하기 위해 '관점'을 들고 해석하는 기법입니다. 결국 중요한 것은 XAI기법 간 미세한 차이를 인식하고 제대로 된 질문을 던져야 할 것입니다.
참고자료
[도서] XAI 설명 가능한 인공지능, 인공지능을 해부하다
혼자 공부하면서 정리하는 개념으로 작성하여 많이 부족합니다.
틀린부분이나 첨언해주실 내용 있으시면 댓글 부탁드려요 ^^*
'머신러닝&딥러닝 > 책요약및리뷰' 카테고리의 다른 글
| [혼자공부하는머신러닝+딥러닝] 3. 회귀 알고리즘과 모델 규제 (0) | 2022.06.15 |
|---|---|
| [혼자공부하는머신러닝+딥러닝] 2. 데이터 다루기 (0) | 2022.06.13 |
| [혼자공부하는머신러닝+딥러닝] 1. 마켓과 머신러닝 (0) | 2022.06.10 |
| [XAI 설명가능한 인공지능] 3. 모델 튜닝하기-Xgboost (0) | 2022.05.17 |
| [XAI 설명가능한 인공지능] 1. 'XAI' 개념 및 개발 준비 (0) | 2022.05.16 |
